Unveiling the Beauty of the Ulam Spiral
Introduction:
Mathematics has a unique way of revealing hidden patterns and mysteries in the world around us. One such captivating mathematical discovery is the Ulam Spiral, a visual representation that showcases the intriguing alignment of prime numbers. Named after the renowned mathematician Stanislaw Ulam, this spiral offers a fascinating glimpse into the distribution of prime numbers in a two-dimensional grid. In this blog post, we embark on a journey to explore the beauty and significance of the Ulam Spiral, diving into its history, structure, and the mesmerizing patterns it unveils.
The Origin of the Ulam Spiral:
The story of the Ulam Spiral begins with Stanislaw Ulam, a Polish-American mathematician who made substantial contributions to various fields of mathematics. In the 1960s, while doodling during a boring conference, Ulam stumbled upon an unexpected pattern in his number spiral. He noticed that prime numbers, those indivisible by any number except 1 and themselves, appeared to align along specific lines. This accidental discovery ignited his curiosity and set the stage for the exploration of prime number distribution.
Understanding the Ulam Spiral:
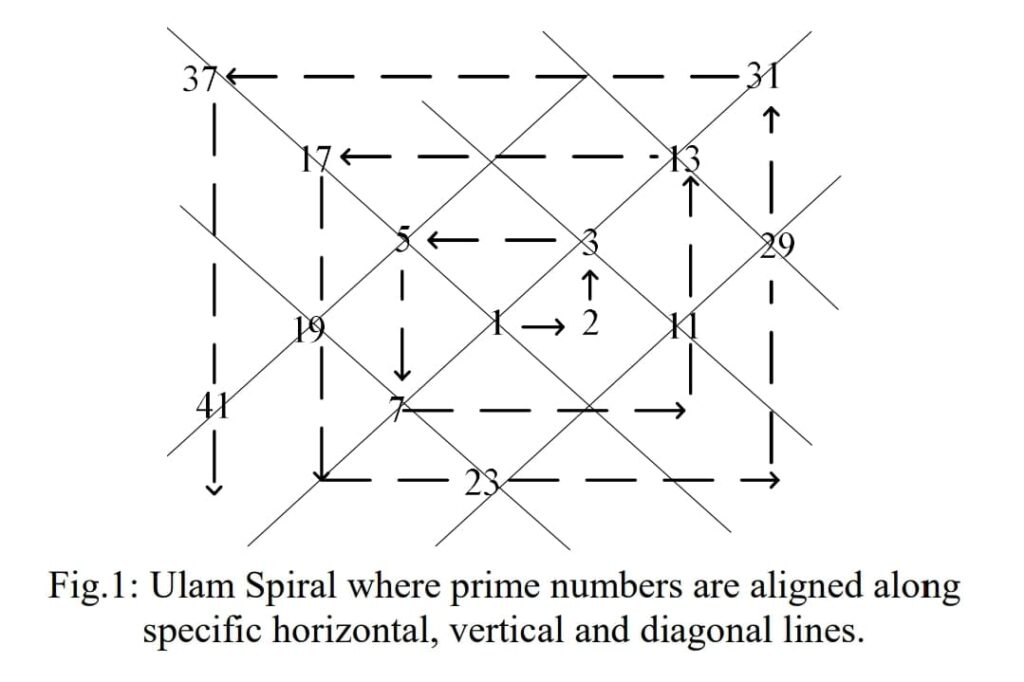
The Ulam Spiral is essentially a grid of numbers, arranged in a spiral pattern, where each integer is placed in a cell. Starting from the center with the number 1, the spiral radiates outward, spiraling through positive integers. The real magic happens when you mark the prime numbers on this grid. To everyone’s amazement, prime numbers often appear along certain horizontal, vertical, and diagonal lines. These patterns are not random but rather reveal hidden order within the world of prime numbers.
The Mesmerizing Patterns:
As you explore the Ulam Spiral, you’ll notice striking patterns emerging. Diagonal lines known as “Ulam’s diagonals” are particularly fascinating, with primes seeming to align along them. Some diagonal lines exhibit regularity, while others display a more intricate arrangement. The Ulam Spiral thus showcases the delicate balance between order and complexity in prime number distribution.
Why the Ulam Spiral Matters:
The Ulam Spiral isn’t just a mathematical curiosity; it has practical implications. It’s used in number theory and cryptography, aiding in the study of prime numbers and their applications in encryption and data security. Understanding prime number distribution is crucial for various mathematical and computational endeavors.
Conclusion:
In the world of mathematics, the Ulam Spiral stands as a testament to the beauty of unexpected discoveries and the elegance of prime numbers. It reminds us that patterns and mysteries are waiting to be uncovered, even in the most unexpected places. As we conclude our journey through the Ulam Spiral, we encourage you to explore this mathematical wonder for yourself, and who knows, you might stumble upon the next hidden gem of mathematical beauty.
Thomas Young’s Double-Slit Experiment: A Journey into the Nature of Light

Introduction:
The study of light has long captivated scientists and thinkers, from ancient philosophers to modern physicists. One pivotal moment in this quest to understand the nature of light was Thomas Young’s double-slit experiment. Through a simple yet profound setup, Young demonstrated that light exhibits wave-like properties, fundamentally changing our understanding of optics. In this blog post, we embark on a journey through the historical and scientific significance of Thomas Young’s groundbreaking experiment, exploring how it unveiled the wave nature of light.
The Quest to Understand Light:
Throughout history, the nature of light was a subject of intense speculation and debate. Some believed it consisted of particles, while others proposed it behaved as waves. The mystery of light’s true nature lingered until the 19th century, when Thomas Young devised an ingenious experiment that would settle the debate once and for all.
Young’s Experiment Unveiled:
Thomas Young’s double-slit experiment, conducted in the early 1800s, involved shining light through two closely spaced slits onto a screen. What he observed on the screen was nothing short of astonishing: an interference pattern of alternating bright and dark fringes. This pattern could only be explained if light exhibited wave-like behavior, as waves can interfere with each other constructively and destructively.
The Wave-Particle Duality:
Young’s experiment introduced the concept of wave-particle duality, suggesting that light could exhibit both wave-like and particle-like properties, depending on how it was observed. This profound idea revolutionized our understanding of not only light but also matter, eventually leading to the development of quantum mechanics.
Impact on Science and Technology:
The implications of Young’s experiment extended far beyond the realm of optics. It laid the foundation for wave theory, which became central to understanding various physical phenomena. Today, we use the principles Young discovered in fields as diverse as quantum mechanics, astronomy, and even the design of advanced optical devices like lasers and holograms.
Conclusion:
Thomas Young’s double-slit experiment remains a milestone in the history of science. It unveiled the wave-like nature of light and forever changed our perception of the universe. It serves as a reminder that sometimes, simple yet ingenious experiments can unlock profound truths about the natural world. As we conclude our journey into the experiment that reshaped our understanding of light, we invite you to appreciate the beauty and elegance of scientific exploration and discovery, where even a beam of light can reveal the secrets of the cosmos.
The Intricate World of Interference Patterns
Introduction:
The natural world is brimming with captivating phenomena, and among them, interference patterns stand as one of the most mesmerizing. These intricate patterns, born from the convergence of waves, create visually stunning and often fractal-like designs. In this post, we’ll embark on a journey to explore the world of interference patterns, from their formation to their mathematical intricacies. Get ready to be captivated by the beauty and science of wave interference.
Waves and Interference:
To understand interference patterns, we first need to grasp the concept of waves. Waves are disturbances that propagate through a medium or space, carrying energy with them. When two or more waves overlap, they interfere with each other, resulting in changes in amplitude and sometimes cancelation or reinforcement of the waves.
Creating Interference Patterns:
Interference patterns occur when waves from different sources meet. These sources could be anything from water waves in a pond to light waves passing through slits. The interaction of these waves leads to regions of constructive interference (where waves reinforce each other) and destructive interference (where waves cancel each other out). This creates a distinctive pattern of alternating bright and dark areas.
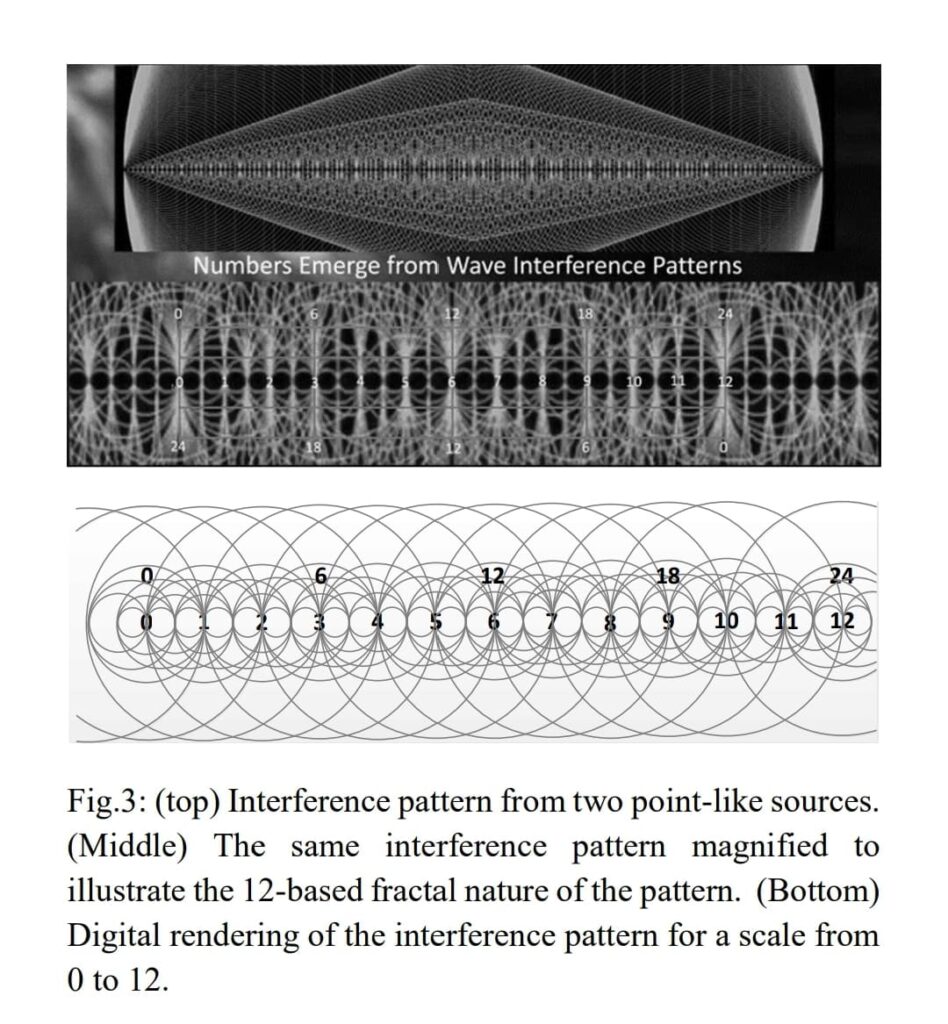
Fractal-Like Complexity:
What makes interference patterns even more fascinating is their propensity to exhibit fractal-like complexity. When you zoom in on an interference pattern, you’ll discover smaller versions of the same pattern, repeating recursively. This self-similarity is reminiscent of the intricate details found in natural phenomena like snowflakes and ferns.
Applications in Science and Art:
Interference patterns are not just a visual treat; they have practical applications. In physics, they help scientists study wave behavior, from sound waves to quantum mechanics. In art, artists have drawn inspiration from these patterns to create captivating visual experiences, and they play a significant role in fields like holography and optics.
Conclusion:
Interference patterns are a testament to the beauty of nature’s hidden intricacies. They remind us that even in the most seemingly simple phenomena, there lies a world of complexity and elegance. Whether you’re an artist looking for inspiration, a physicist exploring the fundamental laws of nature, or simply a curious observer of the world, interference patterns invite you to marvel at the wonders of wave behavior and the captivating dance of light, sound, and waves. As we conclude our journey into this mesmerizing world, we encourage you to seek out and appreciate the artistry and science that surrounds us in everyday life.
The Wave Matrix: Where Mathematics Meets Music and Prime Numbers

Introduction:
In the realm of mathematics, there are moments when disparate fields converge, creating something truly extraordinary. One such marvel is the wave matrix, a complex web of patterns generated by point-like sources. What sets this mathematical wonder apart is its ability to bridge the worlds of mathematics, music, and prime numbers. In this post, we embark on a journey into the wave matrix, exploring its connection to prime number symmetry, musical notes, and the captivating beauty of mathematical patterns.
The Genesis of the Wave Matrix:
The wave matrix originates from the interplay of waves emanating from point-like sources. When these waves interact, they create intricate patterns that transcend the boundaries of regular mathematics. What emerges is a mesmerizing tapestry of interconnected lines, nodes, and symmetry.
Prime Number Symmetry:
One of the most remarkable aspects of the wave matrix is its connection to prime numbers. Prime numbers, those indivisible by any number except 1 and themselves, have long fascinated mathematicians. The wave matrix reveals prime number symmetry, showing that prime numbers are not randomly distributed but instead possess their own order within the matrix.
Musical Notes Correspondences:
The wave matrix also dances to the rhythm of music. Within its patterns lie correspondences to musical notes. This unexpected link between mathematics and music adds a layer of artistry to the already intricate structure of the matrix. It demonstrates that the beauty of mathematics extends beyond numbers and equations.
Digital Rendering:
Modern technology allows us to create digital renderings of the wave matrix, bringing its complex beauty to life. These renderings unveil the intricacies and symmetries within the matrix, making it accessible for exploration and appreciation by both mathematicians and enthusiasts.
The Beauty of Mathematical Intersection:
The wave matrix exemplifies the enchanting intersections of different branches of mathematics. It shows that seemingly unrelated concepts can come together to create something greater than the sum of their parts. It’s a testament to the creativity and curiosity of mathematicians who seek to unravel the mysteries of the universe.
Conclusion:
As we conclude our journey into the world of the wave matrix, we invite you to explore its intricate patterns, prime number symmetries, and musical connections. It serves as a reminder that mathematics is not just a tool for solving problems but a canvas upon which beauty, creativity, and unexpected discoveries can thrive. Whether you’re a mathematician, musician, or simply a lover of all things wondrous, the wave matrix beckons you to explore the boundless possibilities that arise when mathematics meets art and science.